みなさんこんにちは!NY予備校の嶋谷です!
そろそろ慶應義塾ニューヨーク学院では秋AO入試の出願期限が近づいてきました。
出願をした皆さんはここから本格的に試験勉強を始めるかと思います。そこで今回のブログではニューヨーク予備校で実施している模擬試験の数学の問題を一部紹介し、解説をしたいと思います。
問題
問1
1から50までの自然数の中で、2, 3, 5のいずれかで割り切れるものの個数を求めよ。
問2
箱の中にくじが12本入っていて、4本が当たりくじである。この中から3本のくじを同時に取り出すとき、少なくとも1本は当たりくじである確率を求めよ。
自信のある人は一旦ここでスクロールを止めて、紙と鉛筆を用意して解いてみてください
いかがですか?解けましたか?では、解説をしたいと思います。
解説
問1
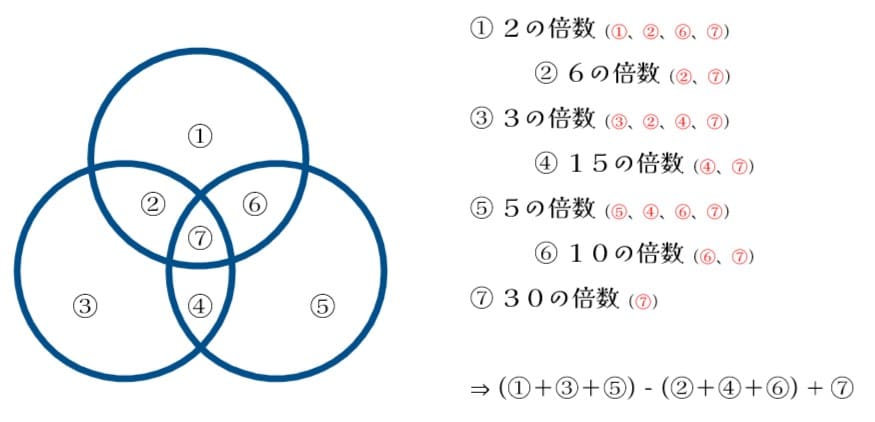
今回の問題では1から50までの自然数の中で2, 3, 5 いずれかで割り切れるものの個数を聞かれているので、「2, 3, 5 の倍数の個数の合計から被っている部分を引け」ばよいことが分かります。(下記のベン図を参照)
①:2の倍数の個数は… 50÷2=25
③:3の倍数の個数は… 50÷3=16 … 2
⑤:5の倍数の個数は… 50÷5=10
②:2の倍数と3の倍数が被っている数字 = 6(2, 3の最小公倍数)の倍数の個数は… 50÷6=8 … 2
④:2の倍数と5の倍数が被っている数字 = 10(2, 5の最小公倍数)の倍数の個数は… 50÷10=5
⑥:3の倍数と5の倍数が被っている数字 = 15(3, 5の最小公倍数)の倍数の個数は… 50÷15=3 … 5
ただしこのまま (25+16+10)-(8+5+3) と計算してしまうと全てにおいて被っている30(⑦)を含めないことになってしまうので最後に 1 を足す必要があります。
よって、(25+16+10)-(8+5+3)+(1) = 36
36個となるわけです。
問2
今回の問題のポイントは問題文に「少なくとも」と記載されていることです。
「少なくとも」と言われたら余事象を考えるようにしましょう。
少なくとも一本は当たりくじ ⇔ 全体から一本も当たりくじが出ない確率を引けばいい
(余事象を考えると計算の場合分けが必要なくなるので簡単になる)
全体の場合の数は12本から3本を選ぶから
12C3 = (12×11×10) / (1×2×3) = 220
一本も当たりくじが出ない場合の数は、8本の外れくじから3本を選ぶことと同義だから
8C3 = (8×7×6) / (1×2×3) = 56
すなわち、全体から一本も当たりくじが出ない確率は、
56/220=14/55
全体から一本も当たりくじが出ない確率(14/55)を引くと
1-14/55=41/55
41/55となります。
いかがでしたか。
今回はニューヨーク予備校で実施している数学模試を紹介しました。ニューヨーク予備校では、この他にも様々な試験対策を行っています。
次回のブログも是非チェックしてみてください。
その他、慶應義塾ニューヨーク学院についてご不明な点等ございましたら、以下のお問い合わせフォームよりお気軽にお問い合わせください。
また、受験に関してのご相談や、本塾への入塾をご希望されている方は、
下記の番号までご連絡よろしくお願いいたします。
<p class=”” style=”text-align: left; background: #eee; width: fit-content; padding: 40px 80px; margin-top: 20px;”>ニューヨーク予備校
お電話でのお問い合わせはこちらへ
<a href=”tel:03-6240-2902″>03-6240-2902
</a>9:00<span class=”s2″>~</span>18:00<span class=”s2″>(平日のみ)</span></p>